Форматы и размеры бумаги — ПБ «Дело в гору». Лист бумаги можно сложить пополам не более определенного числа раз Английские форматы бумаг

Форматы и размеры бумаги — ПБ «Дело в гору». Лист бумаги можно сложить пополам не более определенного числа раз Английские форматы бумаг

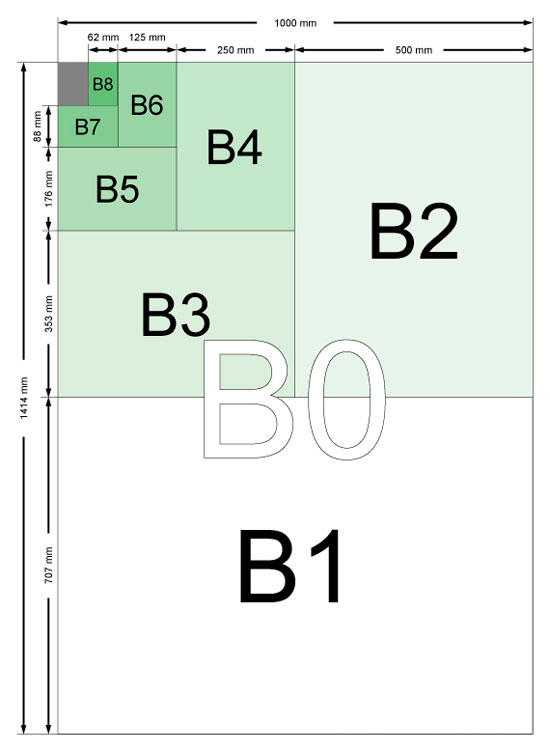
Каждый формат серии B является средним геометрическим между форматами An и A(n+1).

Все размеры бумаг серии B строятся от листа A0, ширина которого равна 1 м.

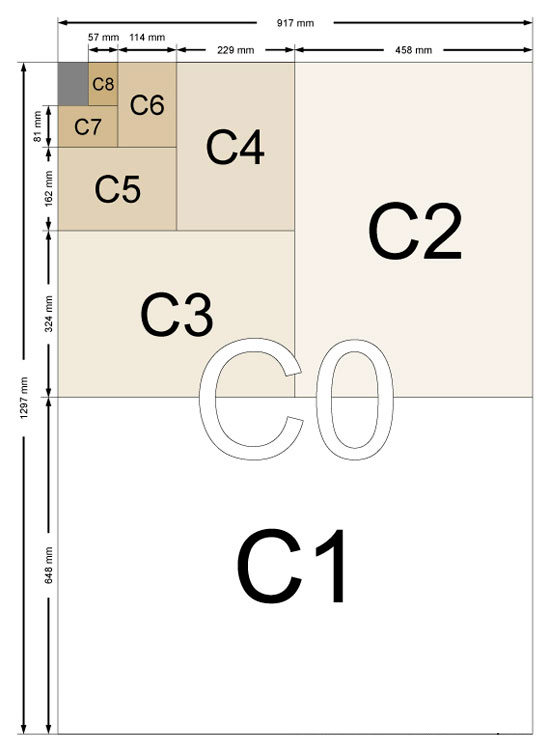
Серия C. Размеры конвертов в склеенном (сложенном виде).

Каждый формат серии C является средним геометрическим между форматами A и B с этим же номером. Благодаря этому лист A4 свободно укладывается в конверт C4.

Допустимое отклонение составляет ±1.5мм для значений до 150мм, ±2мм для значений от 150мм до 600мм, и ±3мм для значений свыше 600мм.

Типичные области применения форматов ISO 216

Дробные форматы, как доля форматов стандарта ISO 216

Обычно такие размеры приобретает разрезанная или сложенная бумага, а также специально изготовленная бумага (например открытки, приглашения).

Размеры форматов по ISO 7810

Стандарт определяет размеры идентификационных визитных карточек.

ISO 623

Стандарт определяет размеры папок для хранения листов А4 и прочей полиграфической продукции не превышающей размеры А4 формата в развернутом или сложенном виде. Даны максимальные размеры для папок в сложенном виде.

ISO 838

Стандарт определяет отверстия в листах под подшивку. Два отверстия диаметром 6±0.5мм. Центры отверстий находятся на расстоянии 80±0.5мм друг от друга и на расстоянии 12±1мм до края листа. Отверстия расположены симметрично относительно оси листа.

Российские стандартные форматы изданий по ГОСТ 5773-90

Американские форматы бумаг

Английские форматы бумаг

Примечание

Эти размеры не распространяется на форматы альбомов, атласов, книжек-игрушек, буклетов, факсимильных, библиофильских, нотных изданий, календарей, изданий, выпускаемых на экспорт, изданий, печатаемых за рубежом, а также миниатюрных, уникальных и экспериментальных изданий.

Формат изданий условно обозначают размером листа бумаги для печати в сантиметрах и долей листа.

Форма издания в миллиметрах определяют: для издания в обложке — его размерами после обрезки с трех сторон, для издания под переплетную крышку — размерами обрезанного с трех сторон блока, при этом первая цифра обозначает ширину, а вторая — высоту издания.

Максимальные форматы являются предпочтительными для применения. Допускается уменьшение формата издания до минимального по высоте и (или) ширине при печатании издания на машинах устаревших конструкций, импортном оборудовании, а также с учетом технологических особенностей производства.

Предельные отклонения форматов изданий от установленного для данного тиража не должны быть более 1 мм по ширине и высоте блока.

Форматы и размеры бумаги — ПБ «Дело в гору». Лист бумаги можно сложить пополам не более определенного числа раз Английские форматы бумаг

Фразу, «лист бумаги нельзя сложить больше семи раз» можно понимать двояко. Во-первых, в том смысле, что это запрещено или существует какое-то поверье типа, если вы сложите лист бумаги 7 раз — случится несчастье. Об этом нигде нет информации.

Тогда эта фраза прозвучит так: «Невозможно сложить любой лист бумаги больше 7 раз». Становится интересно. И многие начинают пробовать складывать листы бумаги: тетрадный листок, стандартный лист А4, газетные полосы, салфетки. Благо бумага у всех под рукой. И почему же бумагу нельзя сложить больше 7 раз ?

Что получится если сложить бумагу 7 раз?

Уже при сложении в пятый раз начинаешь испытывать проблемы, шестое тоже получается с усилием. Седьмой раз складываем и с трудом и получаем толстый кусок бумажного многослойного «прямоугольника», который далее сложить, пополам никак не удается.

Возникает множество вопросов. Неужели существует такое ограничение? Есть ли предел сложения бумаги пополам? И главное, почему нельзя сложить бумагу больше 7 раз?
Кроме практического способа ответа на этот вопрос, можно объяснить «феномен» теоретически. Попробуем посчитать, сколько слоев в этом куске «неподдающейся бумаги. Сначала был одинарный лист бумаги, затем 2 слоя, потом 4 и так далее. При пятикратном сложении получим уже 32 слоя, 6-кратном 64, 7-кратном — 128!. То есть при восьмом сложении мы должны одновременно согнуть 128 слоя бумаги! Вот в чем дело, количество слоев бумаги растет в геометрической прогрессии. Сложить такой многослойный «пирог» вряд ли кому-то удастся с первого раза.

Кто может сложить бумагу больше 7 раз?

Но нашлись люди, которые попытались опровергнуть такое утверждение. Они рассуждали так: чем больше будет размер первоначальной бумаги, тем легче будет его сложить потом. Это действительно так. Ведь с увеличением размеров бумаги растет плечо силы, с которым мы прикладываем усилие по складыванию бумаги пополам. Это всем известное правило рычага: чем длиннее рычаг, тем больше момент силы, то есть во столько же раз увеличивается наша сила. Поэтому исследователи берут как можно большое по площади листы бумаги (вплоть до размеров футбольного поля) и складывают его. Правда при этом им приходится пользоваться техническим средствами (каток и погрузчик). В этом эксперименте им удалось сложить бумагу пополам 8 раз вручную, 11 раз с помощью техники.

Еще один способ развеять этот «миф» взять как можно более тонкий лист бумаги. И в этом опыте исследователям удалось превзойти предел равный семи. Тонкая калька (от офсетной бумаги) складывается 8 раз, с усилиями.

Итак, выводы. Поверье о том, что бумагу нельзя сложить более 7 раз пополам возникло не на пустом месте. Действительно складывать бумагу с каждым разом становится все труднее и труднее. Во всяком случае, существует предел складывания бумаги, одни говорят, что оно равно 7, другие 8 или более, но суть одна: бумагу нельзя сложить пополам бесконечное множество раз.

Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания – 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».

Разумеется, мы говорим о бумаге реальной, имеющей конечную, а не нулевую, толщину. Если складывать её аккуратно и до конца, исключая разрывы (это очень важно), то «отказ» складываться вдвое обнаруживается, обычно, уже после шестого раза. Реже – седьмого. Попробуйте проделать это с листком из тетради.

И, как ни странно, от размеров листа и его толщины ограничение мало зависит. То есть, просто так взять тонкий лист побольше, да и сложить его вдвое, раз допустим 30 или хотя бы 15 – не получается, как ни бейся.

В популярных подборках, типа «А знаете ли вы что…» или «Удивительное рядом», факт сей — что вот больше именно 8 раз сложить бумагу нельзя — до сих пор можно найти очень во многих местах, в Сети и вне. Но факт ли это?

Давайте рассуждать. Каждое сложение удваивает толщину кипы. Если толщину бумаги принять равной 0,1 миллиметра (размер листа мы сейчас не рассматриваем), то сложение её вдвое «всего» 51 раз даст толщину сложенной пачки в 226 миллионов километров. Что уже очевидный абсурд.

Мировая рекордсменка Бритни Гэлливан и бумажная лента, сложенная вдвое (в одном направлении) 11 раз (фото с сайта mathworld.wolfram.com).

Кажется, тут-то мы начинаем понимать, откуда берётся известное многим ограничение на 7 или 8 раз (ещё раз – бумага у нас реальная, она не тянется до бесконечности и не рвётся, а порвётся – это уже не складывание). И всё же…

В 2001 году одна американская школьница решила вплотную заняться проблемой двойного складывания, а получилось из этого целое научное исследование, да ещё и мировой рекорд.

Собственно, началось всё с вызова, брошенного педагогом ученикам: «А вот попробуйте сложить хоть что-нибудь пополам 12 раз!». Мол, убедитесь, что это из разряда совершенно невозможного.

Бритни Гэлливан (Britney Gallivan) (заметим, сейчас она уже студентка) поначалу отреагировала как Алиса Льюиса Кэрролла: «Бесполезно и пробовать». Но ведь говорила Алисе Королева: «Осмелюсь сказать, что у вас не было большой практики».

Вот Гэлливан и занялась практикой. Порядком намучившись с разными предметами, она сложила-таки лист золотой фольги вдвое 12 раз, чем посрамила своего преподавателя.

Пример складывания листа вдвое четыре раза. Пунктир – предыдущее положение трёхкратного сложения. Буквы показывают, что точки на поверхности листа смещаются (то есть, листы скользят друг относительно друга), и занимают в результате не то положение, как может показаться при беглом взгляде (иллюстрация с сайта pomonahistorical.org).

На этом девушка не успокоилась. В декабре 2001 года она создала математическую теорию (ну, или математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, используя ряд правил и несколько направлений складывания (для любителей математики, несколько подробнее — ).

Бритни заметила, что к этой проблеме ранее уже обращались математики, но правильного и проверенного практикой решения задачи ещё никто не предоставлял.

Гэлливан стала первым человеком, который правильно понял и обосновал причину ограничений на сложение. Она изучила накапливающиеся при складывании реального листа эффекты и «потерю» бумаги (да и любого иного материала) на сам сгиб. Она получила уравнения для предела складывания, для любых исходных параметров листа. Вот они.

Первое уравнение относится к складыванию полосы только в одном направлении. L — минимально возможная длина материала, t – толщина листа, и n — число выполненных сгибов в два раза. Разумеется, L и t должны быть выражены в одних и тех же единицах.

Гэлливан и её рекорд (фото с сайта pomonahistorical.org).

Во втором уравнении речь идёт о складывании в различных, переменных, направлениях (но всё равно – вдвое каждый раз). Здесь W – ширина квадратного листа. Точное уравнение для складывания в «альтернативных» направлениях – более сложное, но здесь приводится форма, дающая очень близкий к реальности результат.

Нам так и не удалось найти первоисточник этого широко распространённого поверья: ни один лист бумаги нельзя сложить вдвое больше семи (по некоторым данным — восьми) раз. Между тем текущий рекорд складывания — 12 раз. И что удивительнее, принадлежит он девушке, математически обосновавшей эту «загадку бумажного листа».

Разумеется, мы говорим о бумаге реальной, имеющей конечную, а не нулевую, толщину. Если складывать её аккуратно и до конца, исключая разрывы (это очень важно), то «отказ» складываться вдвое обнаруживается, обычно, уже после шестого раза. Реже — седьмого. Попробуйте проделать это с листком из тетради.

И, как ни странно, от размеров листа и его толщины ограничение мало зависит. То есть, просто так взять тонкий лист побольше, да и сложить его вдвое, раз допустим 30 или хотя бы 15 — не получается, как ни бейся.

В популярных подборках, типа «А знаете ли вы что…» или «Удивительное рядом», факт сей — что вот больше именно 8 раз сложить бумагу нельзя — до сих пор можно найти очень во многих местах, в Сети и вне. Но факт ли это?

Давайте рассуждать. Каждое сложение удваивает толщину кипы. Если толщину бумаги принять равной 0,1 миллиметра (размер листа мы сейчас не рассматриваем), то сложение её вдвое «всего» 51 раз даст толщину сложенной пачки в 226 миллионов километров. Что уже очевидный абсурд.

Кажется, тут-то мы начинаем понимать, откуда берётся известное многим ограничение на 7 или 8 раз (ещё раз — бумага у нас реальная, она не тянется до бесконечности и не рвётся, а порвётся — это уже не складывание). И всё же…

В 2001 году одна американская школьница решила вплотную заняться проблемой двойного складывания, а получилось из этого целое научное исследование, да ещё и мировой рекорд.

Бритни Гэлливан (Britney Gallivan) (заметим, сейчас она уже студентка) поначалу отреагировала как Алиса Льюиса Кэрролла: «Бесполезно и пробовать». Но ведь говорила Алисе Королева: «Осмелюсь сказать, что у вас не было большой практики».

Вот Гэлливан и занялась практикой. Порядком намучившись с разными предметами, она сложила-таки лист золотой фольги вдвое 12 раз, чем посрамила своего преподавателя.

Собственно, началось всё с вызова, брошенного педагогом ученикам: «А вот попробуйте сложить хоть что-нибудь пополам 12 раз!». Мол, убедитесь, что это из разряда совершенно невозможного.

Пример складывания листа вдвое четыре раза. Пунктир — предыдущее положение трёхкратного сложения. Буквы показывают, что точки на поверхности листа смещаются (то есть, листы скользят друг относительно друга), и занимают в результате не то положение, как может показаться при беглом взгляде (иллюстрация с сайта pomonahistorical.org).

На этом девушка не успокоилась. В декабре 2001 года она создала математическую теорию (ну, или математическое обоснование) процесса двойного складывания, а в январе 2002 года проделала 12-кратное складывание пополам с бумагой, используя ряд правил и несколько направлений складывания.

Бритни заметила, что к этой проблеме ранее уже обращались математики, но правильного и проверенного практикой решения задачи ещё никто не предоставлял.

Гэлливан стала первым человеком, который правильно понял и обосновал причину ограничений на сложение. Она изучила накапливающиеся при складывании реального листа эффекты и «потерю» бумаги (да и любого иного материала) на сам сгиб. Она получила уравнения для предела складывания, для любых исходных параметров листа. Вот они.

Первое уравнение относится к складыванию полосы только в одном направлении. L — минимально возможная длина материала, t — толщина листа, и n — число выполненных сгибов в два раза. Разумеется, L и t должны быть выражены в одних и тех же единицах.

Во втором уравнении речь идёт о складывании в различных, переменных, направлениях (но всё равно — вдвое каждый раз). Здесь W — ширина квадратного листа. Точное уравнение для складывания в «альтернативных» направлениях — более сложное, но здесь приводится форма, дающая очень близкий к реальности результат.

Для бумаги, которая не является квадратом, вышеупомянутое уравнение всё ещё даёт весьма точный предел. Если бумага, скажем, имеет пропорции 2 к 1 (по длине и ширине), легко сообразить, что нужно сложить её один раз и «привести» к квадрату двойной толщины, а затем воспользоваться вышеупомянутой формулой, мысленно держа в уме одно лишнее складывание.

В своей работе школьница определила строгие правила двойного сложения. Например, у листа, который свёрнут n раз, 2n уникальных слоёв обязаны лежать подряд на одной линии. Секции листа, не удовлетворяющие этому критерию, не могут считаться как часть свёрнутой пачки.

Так вот Бритни и стала первым в мире человеком, сложившим лист бумаги вдвое 9, 10, 11 и 12 раз. Можно сказать, не без помощи математики.

Возможно это, силен если ты!

Пробовали ли вы когда-нибудь складывать обычный лист бумаги? Вероятно, да. Один, два, три раза — не проблема. Потом уже тяжелее. Стандартный лист бумаги формата А4 вряд ли кто сможет сложить боле 7 раз без подручных средств. Все это объясняется наличием физического феномена — многократно складывать лист бумаги не получается из-за быстроты роста показательной функции .

Как говорит Википедия, количество слоёв бумаги равняется двум в степени n, где n — количество складываний бумаги. Например: если бумагу сложили пополам пять раз, то количество слоёв будет два в степени пять, то есть тридцать два. И для обычной бумаги можно вывести уравнение.

Уравнение для обычной бумаги:

,

Где W — ширина квадратного листа, t — толщина листа и n
В использовании длинной полосы бумаги требуется точное значение длины L :

,

Где L — минимально возможная длина материала, t — толщина листа и n — количество выполненных сгибаний вдвое. L и t должны быть выражены в одних и тех же единицах.

Если взять не обычную бумагу плотностью 90 г/дм3 (или чуть больше/меньше), а кальку или даже золотую фольгу, то сложить такой материал можно чуть более количество раз — от 8 до 12.

«Разрушители легенд» (Mythbusters) как-то решили проверить закон, взяв лист бумаги размером с футбольное поле (51,8×67,1 м). Используя такой нестандартный лист, им удалось сложить 8 раз без специальных средств (11 раз с применением катка и погрузчика). По утверждению поклонников телепередачи, калька от упаковки офсетной печатной формы формата 520×380 мм при достаточно небрежном складывании без усилий складывается восемь раз, с усилиями — девять. При этом каждый из сгибов должен быть перпендикулярен предыдущему. Если сгибать под другим углом, можно добиться того, что количество сгибаний будет чуть большим (но не всегда).

Вот еще немного попыток:

Ну, а что, если складывать лист бумаги не руками, а взять себе в помощники гидравлический пресс? Давайте посмотрим, что тогда выйдет. Учтите только, что ролик — на английском, с очень сильным акцентом (арабским финским).

Обычно такие размеры приобретает разрезанная или сложенная бумага, а также специально изготовленная бумага (например открытки, приглашения).

Пропорции листа а3. Форматы и размеры бумаги — ПБ «Дело в гору»

Практически ежедневно мы используем бумагу в различных целях: при устройстве на работу, заполняя анкету или просто подписывая открытку родным. Но далеко не каждый из нас знает или даже просто задумывается, о том какие же размеры формата А6 в сантиметрах, байтах или дюймах.

Существует несколько систем вычисления европейских стандартов ISO:

А. Площадь основного листа составляет практически 1м 2 .

В. Основная страница отличается от А0 тем, что ширина бумаги В0 равна 1м 2 .

С. Площадь страницы С0 выводится как среднее арифметическое из параметров А0 и В0.

Составляя листовку в электронном или бумажном виде, необходимо не только знать, какой размер формата А6, а и то, сколько нужно отступить от краев страницы, чтобы при печати не испортить открытку.

Практически все текстовые редакторы задают границы листа в автоматическом режиме, но если вам нужно изменить исходные параметры документа или изображения, то перед началом печати в настройках принтера укажите желаемые значения.

В последних версиях Microsoft Office используются североамериканские стандарты, которые практически полностью соответствуют европейским параметрам ISO.

Соответствующий европейский формат

Существуют еще японские стандарты. Для вычисления размера используется специальная система для расчетов, которая называется JIS. Чтобы узнать формат А6 и какой это размер японского стандарта, рекомендуем вам ознакомиться со следующей таблицей:

Из данной таблицы можно узнать, какими габаритами обладает лист А6 в мм в японской системе стандартов.

Японские стандарты листов серии А единичны европейским размерам. Что касается серии В, то они будут немного больше, в 1.5 раза.

Как вычисляется формат А3

В основе вычисления лежит деление основного формата А0 на несколько меньших частей. Таким образом, можно рассчитать следующие габариты страниц (все данные указаны в миллиметрах):

А0 обладает параметрами 841×1189.

А1. Длина/ширина сторон — 594×841.

А2. Длина/ширина сторон — 420×594.

А3. Длина/ширина сторон — 297×420.

А4. Длина/ширина сторон — 210×297.

А5. Длина/ширина сторон — 148×210.

А6. Длина/ширина сторон — 105×148.

А7. Длина/ширина сторон — 74×105.

А8. Длина/ширина сторон — 52×74.

А9. Длина/ширина сторон 37×52.

Страница А6 получается в результате безотходного деления листа А5 на две части без остатков. Такая методика позволяет сохранять соотношения сторон документа или изображения на разных форматах без искажения.

Размер бумаги А6 используют в полиграфии для создания флаеров, визиток, книжек, блокнотов и органайзеров и т.д. Программисты также использую данные параметры, только для них не так важен размер страницы, как ее размер в байтах, мегабайтах или терабайтах.

Для определения размера бумаги А6 в электронном формате можно воспользоваться данной таблицей:

При работе с изображением важную роль играет количество пикселей, которые соответствуют необходимым параметрам, и каким обладает размером А6 в см при печати. Таблица размерности для А4, А5,А6 и А9:

Размер в пикселях

Печатать при разрешении 200 dpi

Фото при разрешении 300 dpi

8,7 x 6,5 см А9(5,20 х 3,70 см)

13,5 x 10,2 см А6(14,80 х 10,50 см)

15,2 x 10,2 см А6(14,80 х 10,50 см)

17,3 x 13 см А5(21 х 14,80 см)

19,4 x 14,5 см А5(21 х 14,80 см)

21,9 x 16,5 см А5(21 х 14,80 см)

23,8 x 17,9 см А5(21 х 14,80 см)

40,6 x 30,5 см A3(42 x 29,7)

27,1 x 20,3 см А4(29,70 x 21 см)

46,3 x 34,7 см A3(42 x 29,7)

30,9 x 23,2 см А4(29,70 x 21 см)

50,8 x 38,1 см A3(42 x 29,7)

33,9 x 25,4 см А4(29,70 x 21 см)

Международные стандарты

Размеры рамки для черчения А6 по ГОСТу определяются по габаритам внешнего контура А0. За основу для расчетов используют бумагу с параметрами 1189х841, площадь которой равна приблизительно 1м 2 . Согласно нормам, эти данные соответствуют стандартам А0.

Гост 2.301-68 устанавливает все допустимые стандарты для всевозможных чертежей и документов в бумажной/электронной форме, которые разрешены нормами составления и ведения документации в международных форматах. Например, формат А6 размеры в см всегда будет иметь размерность 10,5×14,8.

Для тех, кто как-либо связан с архитектурой или строительством, необходимо разбираться в форматах. Сегодня, стандартный А4 используется только для распечатки текста, а для создания разнообразных чертежей или рисунков требуются ватманы. Размер А2 в сантиметрах 21х29,7, он идеально подходит для набросков и выполнения макетов небольшого масштаба.

Что такое формат

Формат – это размер листа бумаги. Они являются одинаковыми для большей части мира, и где бы вы не были, бумага размером А2 будет такой по площади, как и на родине.

В Европе такие стандарты были приняты в середине 20-го века и уже оттуда, распространились по всему миру. До этого, каждое издательство использовало свои размеры. Чаще всего это было «Золотое сечение», которое так любили живописцы и архитекторы эпохи Возрождения, но оно было не очень удобно для типографского дела.

Со временем, стал применяться лист, стороны которого относились друг к другу как единица к квадратному корню из двух. Такой лист, если его сложить пополам, имел такие же параметры, то есть он являлся уменьшенной копией первоначального «куска» бумаги.

В 20-х годах 20 века была принята единая система ISO 216, согласно которой, размеры формата А2 равны 210х297 миллиметров . Еще одним популярным стандартом бумаги является североамериканский, но маркировка этой системы в нашей стране встречается достаточно редко.

Международные стандарты

ISO 216 имеет несколько серий параметров бумаги:

Каждая из них применяется в разных сферах, и адаптирована под требования именно этих отраслей.

За основу принято считать формат А0, имеющий площадь ровно 1м 2 , но он используется только в специфических сферах, в повседневной жизни люди практически не используют его. Уже от него просчитывается каким должен быть, например, лист А2 в сантиметрах или миллиметрах. Каждый последующий формат – это половина предыдущего. То есть, лист размером А2 в см будет четвертая часть от А0.

Самыми популярными являются листы А4. В англоговорящих странах они приняты как стандарт для делового письма. В нашей стране тоже чаще всего используется именно это размер.

Следующим по популярности является — А2. Какой размер имеет лист формата А2 мы уже говорили, а его диагональ равна 364 миллиметра, а площадь – 0,24948 м 2 . Именно такие листы вы можете видеть вокруг себя каждый день – А2 чаще всего используется для печати газет.

Существуют размеры и больше, чем А0, они используются в основном в технических сферах. Более мелкий формат, такой как А5 или А6 применяют для создания блокнотов, тетрадей и прочей канцелярской бумаги.

Система ISO 216 допускает некоторые погрешности в размерах листов. Обычно они не превышают нескольких миллиметров.

Международный стандарт измерения удобен тем, что любой формат можно с легкостью перевести в другой.

Любое изображение можно отредактировать, применив нужный масштаб. Причем можно это сделать как вручную, так и с помощью техники, так как практически все, что мы используем для распечатки, или для представления документов в электронном виде, ориентировано на использование именно европейской системы измерения листов.

Отечественная система

В нашей стране, размеры формата А2 отличаются от принятых по Госту. Но так как используется в основном импортная техника, которая ориентирована на европейские стандарты, Гост отходит на второй план. Система ISO 216 очень актуальна на сегодняшний день.

Несмотря на то, что во всех сферах жизни преобладает техника, она не всегда может выполнить или показать то, что может человек, сколько бы люди ее не совершенствовали. Например, людям, которым часто приходится использовать какие-либо наглядные пособия, очень удобно использовать ватманы размерами А2, так как они имеют оптимальную площадь: достаточно большие, чтобы можно было показать все детали, и в то же время достаточно компактные. Их используют для:

наглядной демонстрации каких-либо данных;

демонстрации таблиц, диаграмм;

Таблица размеров

Высота x Длина (мм)

Высота x Длина (» дюймы)

93.6 x 66.2 » дюймов

28087 x 19866 px

66.2 x 46.8 » дюймов

19866 x 14043 px

46.8 x 33.1 » дюймов

33.1 x 23.4 » дюймов

23.4 x 16.5 » дюймов

16.5 x 11.7 » дюймов

11.7 x 8.3 » дюймов

8.3 x 5.8 » дюймов

5.8 x 4.1 » дюймов

4.1 x. 2.9 » дюймов

2.9 x 2.0 » дюймов

2.0 x 1.5 » дюймов

1.5 x 1.0 » дюймов

Размеры форматов А0, А1, А2, А3, А4, А5, А6. Также другие форматы, в том числе и других стран.

Форматы стандарта DIN (метрические)

Примечания:
1. Площадь формата A0 равна 1 кв. м.
2. Знак «+» в обозначении формата говорит о наличии припуска по сравнению со стандартными размерами. Величина припуска может быть разной.
3. Для рулонной бумаги ширина соответствует узкой кромке формата, то есть A1 означает рулон шириной 594 мм. Длина стандартного рулона для копировальных машин 175 метров.

Форматы англо-американской системы стандартов

Форматы других международных стандартов

Стандартные форматы бумаги

Наибольший стандартный размер, A0, имеет площадь в один квадратный метр и соотношение сторон 1:√2 . Длинная сторона листа имеет длину, равную примерно 1,189 м, длина короткой стороны — это обратное значение от указанной величины, примерно 0,841 м, произведение этих двух длин даёт площадь в 1 м².

Размер A1 получается разрезанием листа A0 вдоль короткой стороны на две равные части, в результате чего отношение сторон сохраняется. Это позволяет получать один стандартный формат бумаги из другого, что было невозможно при использовании традиционных размеров. Сохранение отношения сторон означает также, что при масштабировании изображения от одного формата к другому, сохраняются пропорции изображения.

Помимо серии форматов A, существуют также менее распространённые форматы серии B. Листы формата B имеют такое же соотношение сторон, как серия A. Только B0 имеет ширину в 1 м. Площадь листов серии B является геометрическим средним двух последующих листов серии A. Например, B1 по размеру находится между A0 и A1, с площадью в 0,71 м² . В результате, B0 имеет размеры 1000 × 1414 мм. Серия B почти не используется в офисе, нимеет ряд специальных применений, например, в этих форматах выходят многие постеры, B5 часто используется для книг, также эти форматы применяются для конвертов и паспортов.

Серия C используется только для конвертов и определяется в ISO 269. Площадь листов серии C равна геометрическому среднему листов серий A и B с тем же номером. Например, площадь C4 есть геометрическое среднее от площади листов A4 и Bпри этом С4 немного больше A4, а B4 немного больше С4. Практический смысл этого в том, что лист A4 можно вложить в конверт C4, а конверт C4 можно вложить в плотный конверт B4.
C6 162 x 114 мм — основной почтовый формат конверта советского периода.

Используемые в настоящее время американские форматы опираются на традиционно используемые размеры, и определяются Американским национальным институтом стандартов (ANSI). Наиболее часто в повседневной деятельности используются форматы «Letter», «Legal» и «Ledger»/«Tabloid». Источник формата «Letter» (8,5 × 11 дюймов или 216 × 279 мм) уходит в традицию и точно не известен.
Североамериканские форматы бумаги являются государственными стандартами в США и Филиппинах (однако филиппинский «legal» — 8,5 × 13 дюймов, что отличается от американского «legal»), а также широко используются в Канаде, Мексике и некоторых странах Южной Америки.
В отличие от стандартной бумаги A4, которая является геометрическим подмножеством диапазона форматов бумаги, основанных на стандарте Международной организации по стандартизации (ISO), происхождение размеров бумаги «Letter» теряется в традициях и не является внятно документированным. Американская ассоциация леса и бумаги утверждает, что размеры происходят с дней ручного производства бумаги, и что 11-дюймовая длина страницы это четверть «средней максимальной длины рук опытного рабочего». Однако, это не объясняет ширину или соотношение сторон.

Источники:

http://delovgoru.pro/formaty-i-razmery-bumagi/
http://crpins.ru/formaty-i-razmery-bumagi-pb-delo-v-goru-list-bumagi-mozhno-slozhit.html
http://girlsgameland.ru/polomki/proporcii-lista-a3-formaty-i-razmery-bumagi-pb-delo-v-goru-princip/