Геометрический и физический смысл производной. Определение производной функции, ее геометрический и физический смысл
Содержание
- 1 Геометрический и физический смысл производной. Определение производной функции, ее геометрический и физический смысл
- 1.1 Понятие производной, ее геометрический и физический смысл
- 1.2 «Определение производной, ее физический и геометрический смысл» учебно-методический материал по алгебре (11 класс) на тему
- 1.3 Скачать:
- 1.4 Предварительный просмотр:
- 1.5 Текстовые задачи на наибольшее, наименьшее значение
- 1.6 По теме: методические разработки, презентации и конспекты
- 1.7 Геометрический и физический смысл
- 1.8 Геометрический смысл производной
- 1.9 Физический смысл производной
Понятие производной, ее геометрический и физический смысл
 Рассмотрим функцию у =f(х)., заданную в интервале (а, b); пусть
Рассмотрим функцию у =f(х)., заданную в интервале (а, b); пусть  ,и
,и  тогда приращение функции в точке х выразится формулой
тогда приращение функции в точке х выразится формулой
Производной функции у =f(х) в точке x  называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю.
называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю.
 Производную функции у =f(х) в точке x
Производную функции у =f(х) в точке x  обозначают символом
обозначают символом  (читается: эф штрих от x
(читается: эф штрих от x  ). Следовательно, по определению
). Следовательно, по определению
 или
или
Из формул (1) и (2) следует, что

Формула (4) выражает геометрический смысл производной: производная от данной функции в данной точке равна тангенсу угла между осью Ох и касательной к графику этой функции в соответствующей точке.
Уравнение касательной к линии у =f(х) в точке М(х, у) принимает вид
 (5)
(5)
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если  , то уравнение нормали к линии у =f(х) в точке М(х, у) записывается так:
, то уравнение нормали к линии у =f(х) в точке М(х, у) записывается так:

Физический смысл производной состоит в следующем: производная от пути по времени равна скорости прямолинейного движения точки.
 Если в формуле (2) от точки х перейти к другой точке х, получим другой предел, поэтому
Если в формуле (2) от точки х перейти к другой точке х, получим другой предел, поэтому  — некоторая функция аргумента х:
— некоторая функция аргумента х:
217.138.194.68 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
«Определение производной, ее физический и геометрический смысл»
учебно-методический материал по алгебре (11 класс) на тему

Материал для дистанционного обучения (Алгебра 11 класс)
Скачать:
Предварительный просмотр:
СПб ГОУ СПО «КОР №1»
Материал для дистанционного обучения
«Определение производной, ее физический и
Учитель : Нарижная Ольга Борисовна
Определение производной, ее физический и
Определение. Производной функции по аргументу х, называется предел отношения приращения функции к приращению аргумента , когда стремится к нулю.
Так как мгновенной или истинной скоростью называется предел, к которому стремится ,
когда интервал времени, на котором она измеряется, стремится к нулю, т.е. . Следовательно, физический смысл производной состоит в том, что производная есть скорость изменения данной функции.
Рассмотрим график произвольной функции :
Если ,то Прямая касательной α
Следовательно, геометрический смысл производной состоит в том, что значение производной в точке касания равно тангенсу угла наклона касательной проведенной к графику функции в эту точку.
Процесс нахождения производной называется дифференцированием.
Для нахождения производной от данной функции необходимо провести следующие действия: 1) дать аргументу x приращение , вычислить наращенное значение функции ;2)найти соответствующее приращение функции: ;3) составить отношение приращения функции к приращению аргумента: ;4) найти предел данного отношения при .
Вычислим производные от некоторых элементарных функций.
1. Производная постоянной равна нулю, т.е. если y=C, где C=const, то .
док-во: y=C, следовательно, при любом значении x
Домножим и разделим на x выражение, стоящее в правой части последнего равенства:
Обозначим величину через α. Очевидно, что при и данном x. Следовательно:
Доказывая аналогичными способами можно вывести производные всех элементарных функций.
Таблица производных элементарных функций:
2. 7.
Приведем примеры вычисления производных:
; ; ; ; , следовательно к таблице производных необходимо добавить производную линейной функции:
Теорема 1. Постоянный множитель выносится за знак производной.
Производная суммы конечного числа дифференцируемых функций равна соответствующей сумме производных этих функций.
Производная от произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение первой функции на производную от второй,т.е. если
Производная частного равна дроби, у которой знаменатель есть квадрат знаменателя исходной дроби,а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателю, т.е.
если , то .
Если функция , имеет в некоторой точке х производную , а функция
имеет при соответствующем значении U производную , тогда сложная функция
в указанной точке х, также имеет производную, которая равна
Приведем несколько примеров нахождения производных:
Если вы смогли разобраться как берутся производные, попробуйте сами отработать тренажеры по взятию производной.
Найдите производную функции : Найдите производную функции:
11.
Найдите производную функции: Найдите производную функции:
Одним из основных направлений применения производной является исследование поведения функций. Сформулируем необходимые для этого теоретические положения.
Первый признак существования экстремума: пусть функция непрерывна в некотором интервале содержащем критическую точку , и дифференцируема во всех точках этого интервала. Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при функция имеет максимум. Если же при переходе через точку слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.
Второй признак существования экстремума: Если первая производная в точке равна нулю, а вторая производная отрицательна, то при функция имеет максимум. Если вторая производная положительна, то минимум.
Пример: исследовать на экстремумы функцию
+ max — min +
0 2/5
Так как при х=0 производная не существует, эта точка также является критической. Точка х=0 является точкой максимума функции, а точка точкой минимума функции.
Пример: Исследовать функцию на экстремумы .
Исследуем эту функцию на экстремумы на отрезке , так как она периодическая с периодом 2π .
Решая уравнение, или , находим критические точки Находим вторую производную:
С помощью теории максимума и минимума решаются многие задачи геометрии, механики, биомеханики.
Если вы смогли разобраться, как решаются задачи на применение производной попробуйте выполнить следующие задания:
Найдите экстремумы функций:
Связь свойств функции и производной
Укажите, какому свойству удовлетворяет функция y(x) на отрезке [1;3], если задана ее производная
Укажите, какому свойству удовлетворяет функция y(x) на отрезке [-2;0], если задана ее производная
Укажите, какому свойству удовлетворяет функция y(x) на отрезке [2;8], если задана ее производная
Укажите, какому свойству удовлетворяет функция y(x) на отрезке [-2;-5], если задана ее производная
Текстовые задачи на наибольшее, наименьшее значение
Задача: В правильной треугольной призме диагональ боковой грани равна 2. Найдите наибольшее значение площади боковой поверхности
Схема решения задачи
Решение конкретной задачи
Пусть х – сторона основания призмы
За х принимается любая из неизвестных величин
Выразить все необходимые для решения задачи величины через введенное
Рассмотрим треугольник , тогда по теореме Пифагора
Учитываются не только алгеброические ограничения, но и физические
За функцию принимается та величина, о наибольшем наименьшем которой идет речь
на наибольшее, наименьшее на интервале
На промежутке (0; ] функция возрастает, а на промежутке [ ,2) убывает, следовательно в точке х= функция имеет максимум, а значит принимает в этой точке наибольшее значение на данном интервале
Найти все значения необходимые для ответа на вопрос
Ответ: наибольшее значение площади равно 6
Если вы смогли разобраться в решении текстовых задач попробуйте сделать следующие задачи самостоятельно:
1.Рассматриваются квадраты, вписанные в различные равнобедренные треугольники с боковыми сторонами, равными 1. (одна сторона квадрата лежит на основании). Найдите сторону наибольшего квадрата.
2. Найдите высоту и радиус основания прямого кругового цилиндра наибольшего объема, описанного около единичного шара.
3. Два корабля движутся по параллельным прямым, находящимся на расстоянии 4 км друг от друга. В какой-то момент времени отрезок, их соединяющий, перпендикулярен их курсам. Скорость первого равна 16 кмчас, скорость второго 20 кмчас. С первого корабля отправляется посыльный катер, скорость которого 28 кмчас. Катер доплывает до второго корабля и тут же возвращается обратно. Какое наименьшее время может продолжаться поездка катера, если: а) оба корабля идут в одном направлении; б) корабли идут в противоположных направлениях?
4. В два различных сосуда налиты растворы соли, причем в первый сосудналито 5 кг, а во второй – 20 кг. При испарении воды процентное содержание соли в первом сосуде увеличилось в p раз,а во втором сосуде в q| раз. Известно, что pq=9. Какое наибольшее количество воды могло при этом испариться из обоих сосудов?
По теме: методические разработки, презентации и конспекты
Урок обобщения и систематизации знаний. Осуществляется подготовка к ЕГЭ по заданиям с производной. Используются различные формы работы (фронтальная, групповая, самостоятельная работа учащихся).
Конспект урока повторения №2 по теме «Физический и геометрический смысл производной» в 11 классе.
Данная методическая разработка может быть использована учащимисяпри самостоятельном изучении данной темы,а также при повторении курса алгебры при подготовке к ЕГЭ.
Контрольная работа составлена на 4 варианта.
Самостоятельная работа представлена в 4 вариантах. Состоит из заданий В-7 открытого банка заданий ЕГЭ, профильный уровень.
Данный материал состоит из подробного конспекта урока, презентации и дидактического материала.
Цель: сформировать целостное представление о производной функции, о ее геометрическом и физическом смысле.Задачи:обобщить и систематизировать материал о производной;изучить методы и способы нахождения.
Геометрический и физический смысл
Перед прочтением информации на текущей странице советуем посмотреть видео о производной и её геометрическом смысле
Также смотрите пример вычисления производной в точке
Касательной к линии l в точке М0 называется прямая М0Т — предельное положение секущей М0М, когда точка М стремится к М0 вдоль данной линии (т. е. угол устремится к нулю) произвольным образом.
Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е. Если x = f(t) — закон прямолинейного движения точки, то x’ = f’(t) — скорость этого движения в момент времени t. Быстрота протекания физических, химических и других процессов выражается с помощью производной. Если отношение dy/dх при х->х0 имеет предел справа (или слева), то он называется производной справа (соответственно производной слева). Такие пределы называются односторонними производными. Геометрическое истолкование производной как углового коэффициента касательной к графику распространяется и на этот случай: касательная в данном случае параллельна оси Оу. Операция нахождения производной называется дифференцированием. Источники: http://studopedia.ru/9_203982_ponyatie-proizvodnoy-ee-geometricheskiy-i-fizicheskiy-smisl.html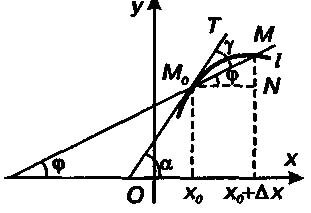 Производной функции у = f
Производной функции у = f 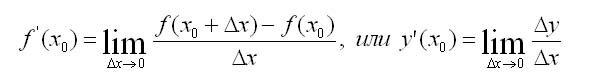 Термин «производная» (а также «вторая производная») ввел Ж. Лагранж (1797), к тому же он дал обозначения y’, f’(x), f”(x) (1770,1779). Обозначение dy/dx впервые встречается у Лейбница (1675).
Термин «производная» (а также «вторая производная») ввел Ж. Лагранж (1797), к тому же он дал обозначения y’, f’(x), f”(x) (1770,1779). Обозначение dy/dx впервые встречается у Лейбница (1675).Геометрический смысл производной
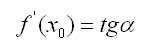 где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.
где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.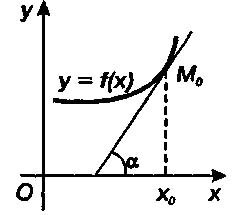 Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид
Уравнение касательной к линии у = f(x) в точке Мо(хо, уо ) принимает вид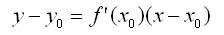 Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линии у = f(x) в точке Мо(хо, уо) запишется так:
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линии у = f(x) в точке Мо(хо, уо) запишется так: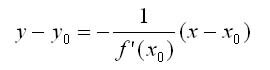
Физический смысл производной
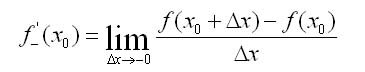
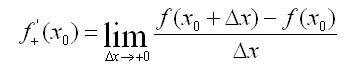 Очевидно, функция f
Очевидно, функция f Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.
http://nsportal.ru/shkola/algebra/library/2015/11/04/opredelenie-proizvodnoy-ee-fizicheskiy-i-geometricheskiy-smysl
http://univer-nn.ru/matematika/geometricheskij-i-fizicheskij-smysl/



