Способы проецирования. Типы проекции изображений в фотографии
Метод начертательной геометрии. Виды проецирования
Изображения на плоскости получают методом проецирования. Аппарат проецирования представлен на рисунке 1.

Рисунок 1. Аппарат проецирования
Объект проецирования — точка А. Через точку А проходит проецирующий луч i с направлением к картинной плоскости, называемой плоскостью проекций. Точка пересечения проецирующего луча с плоскостью проекций называется проекцией точки. Обозначение проекции точки должно содержать индекс плоскости проекций. Например, при проецировании на плоскость Пn проекция точки будет обозначена — Аn.
Виды проецирования
Различают центральное и параллельное проецирование. В первом случае источник лучей находится в обозримом пространстве — точка S собственная, во втором — источник лучей расположен в бесконечности. Схемы центрального и параллельного проецирования приведены соответственно на рисунках 2 и 3. Модель центрального проецирования — пирамида (рисунок 4) или конус; модель параллельного проецирования — призма (рисунок 5) или цилиндр.

Рисунок 2. Схема центрального проецирования
Проецированием на одну плоскость проекций получается изображение, которое однозначно не определяет форму и размеры предмета. На рисунке 1 проекция точки А — Аn не определяет положение самой точки в пространстве, поскольку по одной проекции невозможно определить расстояние, на котором точка находится от плоскости П. Наличие только одной проекции создает неопределенность изображения. В таких случаях, когда невозможно воспроизвести пространственный образ (оригинал) предмета, говорят о необратимости чертежа.

Рисунок 3. Схема параллельного проецирования

Рисунок 4. Модель центрального проецирования (пирамида)
Для исключения неопределенности объекты проецируют на две, три и более плоскостей проекций. Ортогональное проецирование на две плоскости предложил французский геометр Гаспар Монж (ХVIII век). Метод Монжа представлен на рисунке 6,а,б,в (а — наглядное изображение точки в двугранном угле, б — комплексный чертеж точки, в — восстановление объекта, точки А, в пространстве по ее проекциям).

Рисунок 6. Проецирование точки:
а — образование проекций пространственной точки А;
б — чертеж точки А;
в — восстановление пространственного образа точки А по проекциям А1 и А2
Инвариантные свойства параллельных проекций:
- проекция точки есть точка;
- проекция прямой в общем случае прямая;
- проекции взаимно параллельных прямых в общем случае — параллельные прямые;
- проекции пересекающихся прямых — пересекающиеся прямые, при этом точки пересечения проекций прямых лежат на одном перпендикуляре к оси проекций;
- если плоская фигура занимает положение, параллельное плоскости проекций, то она проецируется на эту плоскость в конгруэнтную фигуру.
Различают косоугольные и прямоугольные параллельные проекции. Если проецирующие лучи направлены к плоскости проекций под углом, отличным от прямого, то проекции называют косоугольными. Если проецирующие лучи перпендикулярны к плоскости проекций, то полученные проекции называют прямоугольными. Для прямоугольных проекций используют термин ортогональные от греческого ortos — прямой.
При ортогональном проецировании в пространство вводят две или три взаимно перпендикулярные плоскости, которым присваивают следующие названия и обозначения:
- горизонтальная плоскость проекций — П1
- фронтальная плоскость проекций — П2
- профильная плоскость проекций — П3
Плоскости проекций бесконечны и, пересекаясь, делят пространство на восемь частей — октантов, как показано на рисунке 7.

Рисунок 7. Три взаимно перпендикулярные плоскости проекций П1, П2 и П3 делят пространство на восемь частей (октантов)
В практике построения изображений чаще всего используют первый октант, который далее будем называть трехгранным углом. Наглядное изображение трехгранного угла приведено на рисунке 8.

Рисунок 8. Трехгранный угол, первый октант
При пересечении плоскостей проекций образуются прямые линии — оси проекций:
Если оси проградуировать, то получится координатная система, в которой легко построить объект по заданным координатам. Система прямоугольных координат была предложена Декартом (ХVIIIв.). Ортогональным проекциям присущи все свойства параллельных проекций. На рисунке 9 показано преобразование трехгранного угла и образование комплексного чертежа точки А.

Рисунок 9. Преобразование трехгранного угла и образование чертежа точки в трех проекциях
а — наглядное изображение, б — развертка трехгранного угла, в — чертеж точки
На рисунке 10 приведен комплексный чертеж прямого кругового конуса, отмечена точка S — вершина конуса. Оси проекций X, Y, Z не показаны, что часто используется в практике построения чертежей.

Рисунок 10. Пример чертежа конуса и принадлежащей точки S. Чертеж выполнен без указания осей проекций
- В.Н. Быкова Г.Д. Мефодьева Л.Я. Мефодьева В.И. Сединин Инженерная и компьютерная графика: Учебное поcобие — Новосибирск: СибГУТИ, 2010
- В.С. Дукмасова, В.А. Краснов МЕТОДИКА РЕШЕНИЯ ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ: Учебное поcобие — Челябинск: Изд. ЮУрГУ, 2006
Вместе со статьей «Метод начертательной геометрии. Виды проецирования» читают:
Способы проецирования. Типы проекции изображений в фотографии
Существует два вида проекций: центральные и параллельные.

Центральное проецирование

Если все проецирующие лучи проходят через одну и ту же точку, проекция называется центральной.
Изображения в центральной проекции передают предмет так, как мы его видим. Примером центральной проекции может служить обычная фотография или тень от предмета, освещение лампой.
На flash-ролике за центр проецирования условно взята электрическая лампочка. Исходящие от неё световые лучи, которые условно приняты за проецирующие, образуют на полу тень, аналогичную центральной проекции предмета.
Для активации flash-ролика кликните по изображению
Метод центрального проецирования используется при построении перспективы. Перспектива даёт возможность изображать предметы такими, какими они представляются нам в природе при рассмотрении их с определенной точки наблюдения.
В машиностроительных чертежах центральные проекции не применяются. Ими пользуются в строительном черчении и в рисовании.
Параллельное проецирование

Если все проецирующие лучи параллельны между собой, проекция называется параллельной.
В зависимости от угла наклона проецирующего луча к плоскости проекций параллельные проекции делятся на прямоугольные, или ортогональные, и косоугольные. Если проецирующие лучи составляют с плоскостью проекций примой угол, то такие параллельные проекции называются прямоугольными.
На flash-ролике показано, как получается параллельная косоугольная и параллельная прямоугольная проекции. Центр проецирования предполагается условно удалённым в бесконечность. Тогда параллельные лучи отбросят на плоскость проекций тень, которую можно принять за параллельную проекцию изображаемого предмета.
Для активации flash-ролика кликните по изображению
Способы проецирования. Типы проекции изображений в фотографии

Раздел 2: Проецирование (6 часов)
Понятие о проецировании. Способы проецирования. Центральное и параллельное проецирование. Прямоугольное (ортогональное) проецирование. Проецирование на 2 и 3 взаимно перпендикулярные плоскости. Метод Монжа. Плоскости проекций. Расположение видов. Аксонометрические проекции. Прямоугольная изометрическая проекция. Способы построения прямоугольной изометрической проекции плоских и объемных фигур. Рациональные построения в изометрии. Технический рисунок. Эскиз. Решение творческих задач.
Урок № 5: Понятие о проецировании. Способы проецирования.

Ботвинников А.Д. § 3, 4 [1]
Степакова В. В. § 12, 13 [3]
Вышнепольский И.С. § 16 [8]
 pdf Презентация «Способы проецирования»
pdf Презентация «Способы проецирования»

 pdf
pdf
Изображения на чертеже выполняют по правилам проецирования. Проецированием называется процесс получения изображения предмета на плоскости – бумаге, экране, классной доске и т. д. Получившееся при этом изображение называют проекцией .
«Проекция» — слово латинское. В переводе на русский язык оно означает «бросать (отбрасывать) вперед».
В основе правил построения изображений на чертеже лежит метод проекций. Метод проекций — отображение геометрической фигуры на плоскость путем проецирования ее (фигуры) точек.
Чтобы построить изображение предмета по методу проекций, необходимо через точки на предмете (например, через его вершины) провести воображаемые лучи до встречи их с плоскостью. Лучи, которые проецируют предмет на плоскость, называются проецирующими .
Плоскость, на которой получается изображение предмета, называется плоскостью проекции .
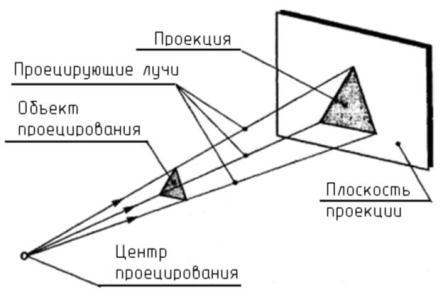
Рис. 1. Понятия проецирования.
Способы изображения предметов отличаются друг от друга, как методами проецирования, так и условиями их построения. Одни способы дают более наглядное изображение, нетрудны для построения, другие менее наглядны, но зато более просты для построения.
Чтобы выяснить, что представляет собой метод проекций, обратимся к примерам.
Поместим перед электрической лампочкой какой-нибудь предмет. Тень, полученную на стене, можно принять за проекцию предмета. Положите на бумагу какой-нибудь плоский предмет и обведите его карандашом. Вы получите изображение, соответствующее проекции этого предмета.
Посмотрим процесс получения проекций геометрических фигур, из которых состоят дорожные знаки (рис. 2, 5, 8). Для построения изображений этих геометрических фигур использован метод проекций.
На рисунке 2,б проекцией точки А будет точка а, т.е. точка пересечения проецирующего луча Оа с плоскостью проекций. Проекцией точки В будет точка b и т. д. Если теперь соединить на плоскости эти точки прямыми линиями, то мы получим проекцию изображаемой фигуры, например треугольника.
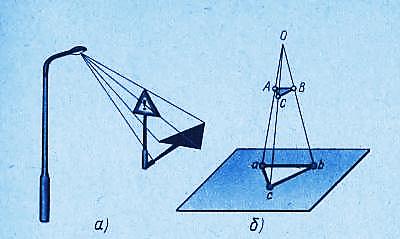
Рис. 2 . Центральное проецирование
На изображениях точки в натуре, т е точки на предмете, будем обозначать большими (прописными) буквами латинского алфавита. Проекции этих точек на плоскость обозначают теми же, но малыми (строчными) буквами.
Рассмотренный пример построения изображений составляют сущность метода проекций.
Если проецирующие лучи, с помощью которых строится изображение предмета, расходятся из одной точки, проецирование называется центральным (рис. 2). Точка, из которой выходят лучи (О), называется центром проецирования. Полученное при этом изображение предмета называется центральной проекцией .
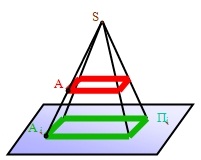
Рис. 3. Центральное проецирование на плоскости.
Величина проекции зависит от положения предмета по отношению к картинной плоскости, а также от расстояния его до этой плоскости и до центра проецирования. На рис. 3, а предмет расположен между центром О и картинной плоскостью К и поэтому его изображение получается увеличенным. Если предмет расположить за плоскостью К (рис. 3, б), то изображение получится уменьшенным.
Центральные проекции часто называют перспективой. Взаимно параллельные линии предмета, не параллельные картинной плоскости, проецируются как группа линий, сходящихся в одной точке (рис. 4).
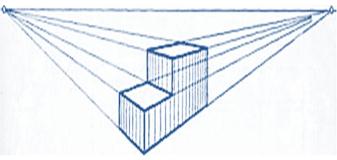
Рис. 4. Перспектива
Проекции каждой группы параллельных линий имеют свою точку схода О 1 и О 2 . Точки схода проекций всех групп параллельных линий расположены на одной прямой, называемой линией горизонта. Предмет, изображенный на рис. 4, расположен по отношению к картинной плоскости так, что ни одна из его граней не параллельна этой плоскости. Такую центральную проекцию называют угловой перспективой.
Изображение, полученное методом центрального проецирования, сходно с фотографией, так как оно получается примерно таким, каким его видит глаз человека. Также примерами центральной проекции являются кинокадры, тени, отброшенные от предмета лучами электрической лампочки, и др. Метод центрального проецирования используется в архитектуре, строительстве, а также в академическом рисовании – рисовании с натуры.
Если проецирующие лучи параллельны друг другу, то проецирование называется параллельным , а полученное изображение – параллельной проекцией . Примером параллельной проекции являются солнечные тени (рис. 5, 8).
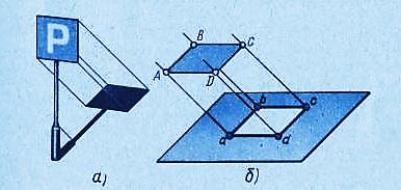
Рис. 5. Параллельное проецирование
При параллельном проецировании все лучи падают на плоскость проекций под одним и тем же углом.
Если это любой угол, отличный от прямого, то проецирование называется косоугольным (рис. 6). В косоугольной проекции, как и в центральной, форма и величина предмета искажаются. Однако строить предмет в параллельной косоугольной проекции проще, чем в центральной.
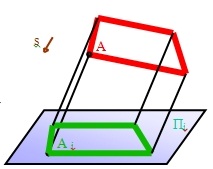
Рис. 6. Параллельное косоугольное проецирование на плоскости.
В техническом черчении такие проекции используют для построения наглядных изображений (рис.7).
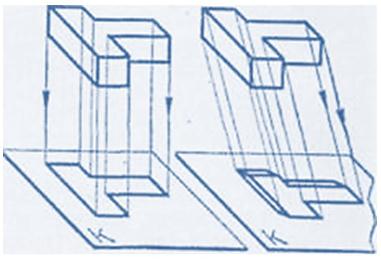
Рис. 7. Процесс поучения наглядного изображения.
В том случае, когда проецирующие лучи перпендикулярны к плоскости проекций (рис. 8), т. ё. составляют с ней угол в 90°. проецирование называют прямоугольным . Полученное при этом изображение называется прямоугольной проекцией предмета.
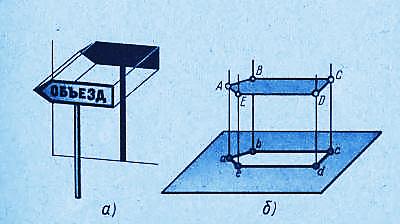
Рис. 8. Параллельное прямоугольное проецирование.
Проекционное черчение имеет большое значение для развития пространственного представления, без которого невозможно сознательно читать чертежи и тем более выполнять их (рис 9).
Прямоугольные проекции называют также ортогональными . Слово «ортогональный» происходит от греческих слов «orthos» — прямой и «gonia» — угол.
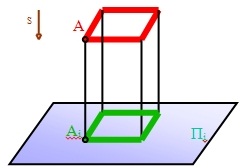
Рис. 9. Параллельное прямоугольное проецирование на плоскости
Способ прямоугольного проецирования является основным в черчении. Он используется для построения изображений на чертежах и наглядных изображений предметов, так как они достаточно наглядны и выполнять их проще, чем центральные.
Чертежи в системе прямоугольных проекций дают достаточно полные сведения о форме и размерах предмета, так как предмет изображается с нескольких сторон.

Практические задания, тесты и домашние работы

Вопросы для повторения

 pdf Вопросы
pdf Вопросы

 ts2
ts2

 pdf Раздели квадрат
pdf Раздели квадрат
 pdf Бочки и ящики
pdf Бочки и ящики
 pdf Часы
pdf Часы
 pdf Занимательные задачи
pdf Занимательные задачи
 pdf
pdf
Источники:
http://digteh.ru/InjGraf/Proec/
http://zhannet.jimdofree.com/%D1%83%D1%87%D0%B0%D1%89%D0%B8%D0%BC%D1%81%D1%8F/%D1%87%D0%B5%D1%80%D1%87%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B8-%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D0%BA%D0%B0/%D0%B2%D0%B8%D0%B4%D1%8B-%D0%BF%D1%80%D0%BE%D0%B5%D1%86%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D1%8F/
http://cherch-ikt.ucoz.ru/index/proecirovanie_2_1/0-9



