Льюис кэрролл годы учения. Ключевые проекты и книги перемен
Содержание
- 1 Льюис кэрролл годы учения. Ключевые проекты и книги перемен
- 1.1 Онтологический музей
- 1.2 Поиск по разделам музея
- 1.3 Последние комментарии
- 1.4 ТУЛЬЧИНСКИЙ Г.Л. Льюис Кэрролл: нонсенс как предпосылка истины
- 1.5 Льюис Кэрролл — Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)
- 1.6 Описание книги «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)»
- 1.7 Похожие книги на «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)»
- 1.8 Льюис кэрролл годы учения. Ключевые проекты и книги перемен
Онтологический музей
Поиск по разделам музея
Последние комментарии










ТУЛЬЧИНСКИЙ Г.Л. Льюис Кэрролл: нонсенс как предпосылка истины
ДУАЛЬНЫЙ ВКЛАД БРИТАНСКОЙ МЕНТАЛЬНОСТИ В ЛОГИЧЕСКУЮ КУЛЬТУРУ
Британская интеллектуальная культура внесла в логику вклад, во многом определивший развитие последней. Причем, вклад, по-своему парадоксальный.
С одной стороны, это реализация свойственной британской ментальности ориентации на здравый смысл, факты, непосредственный опыт. Ориентация эта нашла выражение в теории индукции, развитой Ф.Бэконом, Д.С.Миллем во многом в пику традиционной теории дедукции, восходящей к силлогистике Аристотеля. Для дедуктивного вывода, как известно, необходимо хотя бы одно общее суждение — из двух частных суждений, взятых в качестве посылок, сделать однозначное заключение невозможно. Однако, источник, механизм и правила получения знания, фиксируемого в общих суждениях, до Ф.Бэкона оставались не введенными в логику. Правила же индукции (методы сходства, различия, остатков, сопутствующих изменений) дали такой аппарат, который до сих пор определяет методологию эмпирического знания, интерпретации результатов наблюдения, экспериментов в естествознании, социальных науках, психологии и т.д.
Результатом этого стало осознание, что именно индукция лежит в основе дедукции, потому как формирование общих суждений, в конечном счете, опирается на полную индукцию, т.е. исчерпывающее знание предметов определенной области. Например, в учебниках по логике еще даже конца XIX — начала XX века в качестве бесспорного общеутвердительного суждения приводился пример: «Все лебеди белые». Однако обнаружение в Тасмании популяции черных лебедей обнаружило неполноту и некорректность обобщения. Формирование аппарата индукции показало глубоко и принципиально опытный характер человеческого знания. Логика, при всей ее абстрактности предстала глубоко эмпирической наукой, всегда опирающейся на конкретный уровень человеческого знания. Человек — конечное существо, пытающееся постичь бесконечное — мир во всей бесконечности его разнообразия. Поэтому человеку не дана вся возможная полнота знания. Он всегда постигает мир с какой-то позиции, с какой-то точки зрения, в каком-то смысле.
В этом пункте мы несколько неожиданно сталкиваемся со вторым вкладом британской ментальности в мировую культуру. Речь идет о nonsens’е. Стилистика и поэтика нонсенса, классиками которого являются Э.Лир, Льюис Кэррол, Л.Стерн, Х.Беллок, Э.В.Рью, С.Миллиган, не только и не столько феномен «английского юмора». Последний, действительно, носит несомненный концептуальный характер, являясь преимущественно «игрой ума». В этом его очевидное отличие, например, от немецкого юмора, носящего грубовато-ситуативный характер или от юмора французского — преимущественно словесного.
Дело, однако, не столько в интеллектуально изощренном комизме нонсенса. Это не просто абсурд или черный юмор. Non-sens — отнюдь не отсутствие смысла. Наоборот — он связан с обилием смысловых коннотаций и интерпретаций, умножением, если не факторизацией смысла.
Русскими формалистами (В.Шкловским, Ю.Тыняновым, Б.Эйхенбаумом) в 1914-1920-е годы было убедительно показано, что в основе всякого творческого осмысления лежит остранение — делание привычного непривычным, странным. Следующим шагом является выстраивание из остраненных смыслов нового ряда. Концепция остранения была положена В.Кулешовым, С.Эйзенштейном, самим Б.Шкловским в основу теории монтажа, Б.Брехтом — в основу поэтики театра, Э.Баллоу — в теорию художественного восприятия. Ее коррелятом является концепция лиминальности В.Тернера, согласно которому социально-культурная динамика в любой сфере предполагает стадию лиминальности — устранения социальных статусов, значений, структур и т.д. За нею следует стадия реаггрегации — выстраивания новой структуры. Один из столпов постмодернизма, отец деконструктивизма — Ж.Деррида неоднократно заявлял, что идея деконструкции — не что иное, как переинтерпретированная идея остранения В.Шкловского.
И неспроста, наверное, свою концепцию остранения В.Шкловский вырабатывал, опираясь на анализ творчества не Л.Толстого и особенно — Л.Стерна. По свидетельствам очевидцев, В.Шкловский в то время постоянно носил с собой том «Тристрама Шенди» и читал оттуда фрагменты знакомым при первой же возможности. Аналогично неспроста, думается, и Ж.Деррида, идеи которого не находили поддержки на родине у французской гуманитарной общественности, смог получить ученую степень только защитившись в Британии. Представляется, что в обоих случаях (В.Шкловского и Ж.Дерриды) с очевидностью прослеживается «британский след».
Но есть такая фигура в британской интеллектуальной культуре, в идеях которой обе отмеченные установки — эмпирическая фактичность и нонсенс — не только сочетаются, но и породили нетривиальный логико-семантический синтез. Речь идет о Льюисе Кэрроле.
ШИРОКО ИЗВЕСТНЫЙ НЕИЗВЕСТНЫЙ КЭРРОЛ
Имя Льюиса Кэррола (псевдоним Чарльза Лютвиджа Доджсона) хорошо известно многим, прежде всего, как имя автора «Охоты на Снарка». «Алисы в Стране чудес» и «Алисы в Зазеркалье». [1] Менее известны его логические парадоксы (два из них были в свое время опубликованы в «The Mind») и головоломные задачи, некоторые из которых попали на страницы его сказок. Однако мало кому известно, что автор замечательных сказок и задач, ставящих в тупик не только искушенных в логике людей, но и современные ЭВМ, разработал чрезвычайно оригинальную логическую систему (силлогистики), центральным звеном которой является ее отличное от традиционного семантическое обоснование.
Первое же знакомство с первой частью «Символической логики» Кэррола[2] поражает оригинальностью и глубиной мысли автора, тщательностью и продуманностью не только отдельных положений, но и широкого плана построения целостной логической теории. Сам Кэррол опубликовал только первую часть своего фундаментального труда и ее популярную версию «Логическая игра». Им была подготовлена вторая часть, корректура которой была найдена в архиве профессора Кука Вилсона.[3]
Характерной чертой логической системы Кэррола является то, что она не является плодом чисто умозрительных построений автора. Наоборот, логика Кэррола носит сугубо практический, даже лапидарный характер. Она предназначена для непосредственного решения сложнейших логических и математических задач.[4] Автор сознательно проверяет ее в «экстремальных» случаях, его привлекает прежде всего логический анализ суждений, по меньшей мере странных с точки зрения здравого смысла. Его основная цель — сформулировать предельно общие формулы и правила получения нового знания, которые, подобно улыбке Чеширского кота, остаются после того, как здравый смысл из посылок исчезает.
Глубина поднимаемых Кэрролом логико-философских вопросов, оригинальность их решения отмечались в свое время Б.Расселом, а также представителями таких сравнительно молодых наук, как семиотика и логическая семантика.[5] Речь идет об анализе Кэрролом понятия существования в логике, о возможности получения в его логике заключения из отрицательных посылок, о необычном методе диаграмм, превосходящем эвристическими возможностями хорошо известные диаграммы Л.Эйлера и Д.Венна, об обосновании форм правильного вывода, которые позволяют получать множество новых видов умозаключений, не известных в аристотелевской логике и многом, многом другом.
Несмотря на столь явные достоинства, новаторские идеи и методы Кэррола не были своевременно оценены по достоинству, а имя его незаслуженно обойдено в учебниках по истории логики. Правда, отмечая этот прискорбный факт исторической несправедливости, следует учитывать, что одновременно с автором «Символической логик» (годы жизни Кэррола — 1832-1898) жили и творили такие авторитеты в логике как У.Гамильтон (1788-1856), Д.С.Милль (1806-1873), Г.Лотце (1806-1881), У.Джевонс (1835-1882), А.де Морган (1806-1878), Д.Венн (1834-1923), Г.Фреге и, наконец, основатель современных математических методов в логике — Д.Буль (1815-1864). Творчество Кэррола выпадает как раз на тот период, когда велись активные поиски развития методов формальной логики, по внедрению в логику математических методов, приведших впоследствии к развитию мощного аппарата математической логики. Немудрено поэтому, что логические труды признанного литератора, но мало кому известного преподавателя элементарной геометрии в Оксфорде, остались незамеченными в логической литературе.
Однако вряд ли прав переводчик «Символической логики» на русский язык Ю.Данилов, когда представляет Кэррола самоучкой, не имевшим достаточного логического образования.[6] Кэррол состоял в активной творческой переписке с Д.Венном, им тщательнейшим образом изучена силлогистика Аристотеля. Да и вообще, вряд ли, работая в Оксфорде, он оставался в стороне от современных ему идей математики и логики. О широкой логической эрудиции Кэррола свидетельствует не только глубина его логико-семантических разработок, но и рассыпанные по многим страницам «Символической логик» критические замечания и ответы на возражения возможным, хотя и безымянным критикам. Показательно и само название этой работы. До сих пор считается, что термин «символическая логика» впервые введен в обиход Д.Венном, работа которого, под таким названием вышла впервые в 1881 года, а вторым изданием — в 1894.
Тем не менее, можно сказать, что близкое знакомство с идеями одного из самых оригинальных и интересных британских мыслителей XIX века — дело еще далеко не завершенное, в том числе — в России. Прошла уже почти четверть века с появления первой отечественной работы, посвященной систематическому анализу логики Льюиса Кэррола.[7] За это время найдены и опубликованы материалы III-й и IV-й частей его «Символической логики», вышла на русском языке «Логическая игра»,[8] опубликована серия статей и защищена диссертация Н.Г.Колесникова,[9] эвристический потенциал кэрроловских диаграмм признан не только специалистами по искусственному интеллекту,[10] но и отмечен в энциклопедических изданиях.
Однако логика Кэррола до сих пор остается маргинальной темой в логической литературе. Ряд представляющихся важными и перспективными идей Кэррола, был отмечен в предыдущих публикациях автора данной работы. Время показывает, что обращение к кэрроловскому наследию важно не столько в целях знакомства с его системой, сколько в целях применения некоторых перспектив и возможностей, которые она открывает.
Например, ранее было показано, что только кэрроловские правила силлогистики дают возможность подтверждения гипотезы Я.Лукасевича, согласно которой для того, чтобы отбросить все неправильные модусы аристотелевской силлогистики, необходимо и достаточно аксиоматически отбросить только силлогистическую форму второй фигуры с общеутвердительными посылками и частноотрицательным заключением. Такой модус оказывается содержащим все три кэрроловских правила отбрасывания неправильных модусов, что позволяет строго обосновать интуицию польского исследователя силлогистики.[11] Более того, был продемонстрирован обобщающий характер кэрроловской силлогистики, основанной на двух правилах получения заключения и трех правилах отбрасывания. Это упрощение аксиоматики позволяет достичь как определенную унификацию силлогистических умозаключений с увеличением их количества: 624 правильных и 528 отбрасываемых модусов. Использование дополнительных правил отбрасывания позволяет легко и просто перейти к силлогистикам Лейбница (24 модуса), Аристотеля (19 модусов) и Гильберта (15 модусов). Тем самым был продемонстрирован внелогических характер ограничений этих систем, поскольку в них отбрасываются модусы, содержащие суждения с отрицательными терминами-субъектами, общеотрицательные суждения с отрицательными предикатами, а также общеутвердительные суждения, в которые входят как часть частноутвердительные суждения с отрицательным предикатом. Однако, все указанные модусы вполне допустимы в силлогистике Кэррола, которая, таким образом, оказывается наиболее общей силлогистической системой.[12]
В данной работе публикации продолжено выявление потенциала и перспектив кэрроловских идей, прежде всего — семантического плана.
КЭРРОЛОВСКИЙ МЕТОД ДИАГРАММ
Кэрролом были предложены два метода логического анализа — диаграммы и индексная запись. Причем ведущую эвристическую роль играют диаграммы. Этот метод основан на классификации универсума рассмотрения с помощью конкретных свойств (признаков).

представляет конкретный универсум. Если воспользоваться неким признаком, например, Х, то универсум может быть поделен на две ячейки: X и

Далее можно, взяв другой признак, например, Y разделить универсум на еще две части. Таким образом, мы получим «двухбуквенную» диаграмму Кэррола:
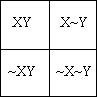
Условимся далее, что знак 1 означает, что данная клетка универсума занята (в ней имеется хотя бы один предмет, наделенный такой комбинацией свойств). Кэррол для это цели чаще использует красную фишку (кружок). Знак 0, стоящий в клетке означает, что эта клетка пуста — таких предметов не существует.
На таких диаграммах можно легко представить простые суждения. Кэррол называет их «суждениями существования» или «нормальными формами». Представим диаграммы для традиционных четырех видов простых суждений: (A) — общеутвердительных (все X есть Y); (E) — общеотрицательных (все X не естьY); (I) — частноутвердительных (некоторые X есть Y) и (O) — частноотрицательных (некоторые X не есть Y):

Некоторые X суть Y = Некоторые Y суть Х = XY существуют = Существуют XY
Льюис Кэрролл — Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)





99 Пожалуйста дождитесь своей очереди, идёт подготовка вашей ссылки для скачивания.
Скачивание начинается. Если скачивание не началось автоматически, пожалуйста нажмите на эту ссылку.
Описание книги «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)»
Описание и краткое содержание «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)» читать бесплатно онлайн.
Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)
Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)
1832, 27 января — родился в деревне Дэрсбери, графство Чешир.
1843 — семья переезжает в деревню Крофт, неподалеку от Ричмонда (графство Йоркшир).
1844-1845 — Школа в Ричмонде.
1845 — Издает «Полезную и назидательную поэзию», первый из «семейных журналов» (опубликован в 1954 г.).
1846 — Поступает в школу Рэгби.
1851, январь — Поступает в Крайст Черч, Оксфорд. Смерть матери, Фрэнсис Джейн Доджсон.
1854, октябрь — Получает степень бакалавра.
1856, 25 апреля — Знакомство с Лориной, Алисой и Эдит Лидделл. Начинает заниматься фотографией.
1857 — Получает степень магистра. Знакомится с Холманом Хаитом, Рэскином.
1858 — Публикует свою первую книгу «Алгебраический разбор Пятой книги Эвклида» (под псевд. «Преподаватель колледжа»).
1859, апрель — Посещает Теннисона в Фаррингфорде, остров Уайт.
1860 — Публикует первую книгу под собственным именем «Конспекты по плоской алгебраической геометрии» Чарлза Лютвиджа Доджсона.
1801, декабрь — Посвящен в сан диакона Сэмюэлом Уилберфорсом, епископом Оксфорда.
1862, 17 июня — Пикник с девочками Лидделл в Нунхеме.
4 июля — Рассказывает сказку об Алисе во время лодочной прогулки в Годстоу дочерям ректора Лидделла.
13 ноября — Начинает работать над рукописью «Приключения Алисы под землей».
1863, 10 февраля — Заканчивает «Приключения Алисы под землей».
1864 — Посылает рукопись «Приключений Алисы под землей» с собственноручными рисунками Алисе Лидделл. Перерабатывает текст в «Алису в Стране чудес».
апрель — Завершает переговоры об издании с художником Тенниелом и с издателем Макмилланом.
1865, 27 июня — Получает от Макмиллана первые экземпляры «Алисы в Стране чудес» (1 изд. «Оксфорд Юниверсити пресс»).
1866 — Публикует «Сведения из теории детерминантов».
1867, 24 января — Первое упоминание в дневнике о работе над «Зазеркальем». Публикует «Элементарное руководство по теории детерминантов».
июль — сентябрь — Едет в Россию с доктором X. Лиддоном.
декабрь — В «Журнале тетушки Джуди» (т. IV) выходит «Месть Бруно» (основное ядро романа «Сильви и Бруно»).
1868, 21 июня — Смерть отца, Чарлза Доджсона.
август — Знакомится с Алисой Рейке, вдохновившей его на «Зазеркалье».
1869, январь — Публикует сб. «Фантасмагория и другие стихи».
12 января — Посылает Макмиллану первую главу «Зазеркалья».
Появляются первые немецкий и французский переводы «Алисы в Стране чудес».
1870, 4 января — Заканчивает рукопись «Зазеркалья».
1871, декабрь — Выходит «Сквозь Зеркало и Что там увидела Алиса» («Алиса в Зазеркалье»).
1872 — Первый итальянский перевод «Страны чудес».
1873, январь — Начинает рассказывать эпизоды о Сильви и Бруно дочерям лорда Солсбери.
1874, июль — Начинает работу над поэмой «Охота на Снарка».
Первый голландский перевод «Страны чудес».
1875, лето — Работает над поэмой «Охота на Снарка» в Сэндауне (остров Уайт).
1876, 29 марта — Выходит в свет «Охота на Снарка». Первая инсценировка «Алисы в Стране чудес» и «Зазеркалья».
1878 — Издает сборник загадок и игр «Словесные звенья».
1879, март — Публикует свой математический труд «Эвклид и его современные соперники»; «Дублеты, словесные загадки». Первый русский перевод «Страны чудес».
1881 — Публикует «Эвклида» (I и II книги). Оставляет пост лектора математики в Крайст Черч.
1882 — Принимает на себя обязанности куратора Клуба преподавателей в Крайст Черч.
1883, 6 декабря — Выход в свет сборника «Стихи? Смысл?».
1884, 5 ноября — Выход в свет «Принципов парламентского представительства».
1885, 22 декабря — Выход в свет «Истории с узелками».
1886, декабрь — Публикует факсимиле рукописи «Приключений Алисы под землей», подаренной Алисе Лидделл. Постановка «Алисы в Стране чудес» в Театре принца Уэльского в Лондоне (постановка Сэвилла Кларка).
1887, 21 февраля — Выход в свет «Логической игры».
1888 — Издает «Математические курьезы» (часть I).
1889, 12 декабря — Выход в свет романа «Сильви и Бруно» (часть I).
1890 — Издает «Алису для детей» и «Круглый бильярд»; «Восемь или девять мудрых слов о том, как писать письма»
1892 — Оставляет пост куратора преподавательского клуба.
1893, 29 декабря — Выход в свет романа «Заключение «Сильви и Бруно»».
Издает вторую часть «Математических курьезов» («Полуночные задачи»).
1890, 21 февраля — Выход в свет «Символической логики» (часть I).
1898, 14 января — Смерть в Гилфорде («Честнатс»).
Похоронен на Гилфордском кладбище.
февраль — Выход в свет сб. «Три заката и другие стихи»,
декабрь — Выход в свет биографии Кэрролла, написанной его племянником Стюартом Доджсоном Коллингвудом.
Похожие книги на «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)»
Книги похожие на «Основные даты жизни и творчества Кэрролла (Чарлза Лютвиджа Доджсона)» читать онлайн или скачать бесплатно полные версии.
Льюис кэрролл годы учения. Ключевые проекты и книги перемен
27 января 1832 года родился английский математик, логик, фотограф, изобретатель Чарльз Лютвидж Доджсон. О человеке, стремившемся сделать математику увлекательной, о логике, любившем нарушать логику, и о любителе писать по ночам рассказываем в сегодняшнем выпуске «Истории науки».
Чарльз Доджсон был как минимум четвертым Чарльзом в роду — вместе с отцом, дедом и прадедом. У его отца, кстати, были неплохие математические способности: он учился в Оксфорде и мог бы построить академическую карьеру, но вместо этого женился и стал приходским священником.
Самый младший из этих Чарльзов пошел по стопам отца: учился в Оксфорде, в том же колледже, что и отец. Он показал себя способным студентом, учеба ему легко давалась, даже несмотря на не самое ответственное к ней отношение.
Особенно отличился он в математике, окончив курс лучшим по этому предмету. После учебы он остался в том же колледже преподавателем. На тех или иных должностях наш герой будет числиться в Оксфорде до конца жизни.
В колледже Чарльз начал свою писательскую карьеру и там же придумал себе псевдоним, под которым мы все его и знаем. С этим Доджсону помог его издатель Эдмунд Йейтс. Идея состояла в том, чтобы найти латинские аналоги имен писателя, Чарльз и Лютвидж, немного их изменить и взять себе как псевдоним.
Наш герой последовал совету: аналог имени Чарльз — Карл — он изменил до Кэрролла, а Лютвидж через Людовика превратился в Льюиса. Ну и, вдобавок, он поменял их местами.
Было еще несколько вариантов псевдонима, например Эдгар Катвеллис (Edgar Cuthwellis), который можно было получить перестановкой букв в тех же Чарльзе и Лютвидже (Charles Lutwidge).
Как говорится в одной из его биографий, «Если бы Доджсон не написал «Алису», его могли бы запомнить как «пионера» фотографии, одного из первых, кто воспринимал фотографию как искусство, а не просто средство фиксирования изображения… Если бы Доджсон не написал «Алису» и не был бы фотографом, его бы помнили как математика, к этой карьере он стремился, будучи лектором Крайст-Черч, крупнейшего колледжа Оксфорда».
Вот об этом фотографе, математике, логике и изобретателе и пойдет сегодня речь. О писателе мы больше не скажем ни слова.
Фотоаппарат появился у Доджсона в 1856 году, он был желанной (и недешевой в то время) покупкой. Фотография сразу увлекла Чарльза. Многие годы он снимал своих друзей и знакомых, взрослых и детей.
Его известность как писателя и навыки фотографа позволили ему заполучить в качестве моделей известных людей того времени: художника и поэта Данте Габриэля Россетти, живописца Джона Милле, писателя и художника Джона Рескина, дарвиниста Томаса Гексли и физика Майкла Фарадея. Да и себя в качестве модели он тоже с охотой привлекал.
Увлечение фотографией в середине XIX века требовало немало терпения и ловкости. Вот как Доджсон описывал в одном из своих рассказов фотографию с выдержкой в минуту и сорок секунд: «Весь дрожа от нетерпения, я спрятал голову под чехол и начал проявлять снимок.
Деревья довольно нечеткие… ладно! Ветер раскачивал ветви, но это не будет очень заметно. А фермер? М-да… он прошел несколько ярдов, и прискорбно видеть, как много рук и ног у него появилось. Бог с ним! Назовем его пауком, сороконожкой, чем угодно… а корова? С большой неохотой я был вынужден признать, что у коровы три головы, и, хотя такое животное имеет курьезный вид, его не назовешь живописным».
Доджсон-математик и логик занимался как «серьезной» наукой, так и составлением математических игр и головоломок. Он предложил графический способ логических задач и способ вычисления определителей матриц, называемый конденсацией Доджсона. Он написал довольно необычную по форме (в виде диалогов) работу о Евклиде, учения которого уже начали ставить под сомнение современники Чарльза.
Помимо этого Чарльз составил множество логических и математических задач для детей, геометрические головоломки, задачки на последовательности. Был среди его книг и «почти серьезный» учебник «Символическая логика». Также широко известны его «Полуночные задачи» (Pillow Problems) — сборник из 72 задач, предназначенных для решения в уме.
Значительная их часть относится к геометрии и теории вероятностей. Вот одна из них: «Урна содержит один шар, о котором известно, что он либо белый, либо черный. В урну кладут белый шар, после чего его содержимое перемешивают и вытаскивают наудачу один шар, который оказывается белым. Какова после этого вероятность вытащить белый шар?»
Доджсон предложил множество маленьких усовершенствований, в разной степени полезных: способ проверки делимости чисел на 17 и 19, два шифра, шкалу для определения количества налитого ликера, мнемонические правила для запоминания цифр, условия исключения из теннисных турниров и шахматы для путешественников.
Также известно его изобретение, позволяющее записывать что-либо в темноте, — никтограф (или тифлограф). Устройство несложное — кусок плотного картона с 16 квадратными вырезами. К нему прилагался шифр, вписывающий каждую букву в квадратик никтографа. Используя эту систему, Доджсон мог записывать пришедшие в часы бессонницы мысли (или те же «Полуночные задачи»), не утруждая себя поисками свечи.
Еще одна его выдумка — игра в слова, или дуплеты. Суть ее состоит в выстраивании цепочки слов между двумя данными в условии, чтобы каждое последующее отличалось от предыдущего лишь одной замененной буквой.
Само собой, все слова будут существительными, а количество и порядок букв менять нельзя. Примером таких дуплетов (пар первое/последнее слово) могут служить «волк и нора», «море и суша» или «four и five».
Источники:
http://ontology.mirtesen.ru/blog/43251363880
http://www.libfox.ru/26413-lyuis-kerroll-osnovnye-daty-zhizni-i-tvorchestva-kerrolla-charlza-lyutvidzha-dodzhsona.html
http://weekend.rambler.ru/read/38908547-chto-pridumal-i-otkryl-lyuis-kerroll/



