Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

преобразования логических выражений

Логические выражения называются равносильными, если их истинностные значения совпадают при любых значениях, входящих в них логических переменных. В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений. Приведем соотношения, отражающие эти законы.

1. Закон двойного отрицания:

А = 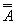. Двойное отрицание исключает отрицание.

2. Переместительный (коммутативный) закон:

— для логического сложения: А к B = B к A ;

— для логического умножения: A & B = B & A .

Результат операции над высказываниями не зависит от того, в каком порядке берутся эти высказывания.

В обычной алгебре a + b = b + a, a Д b = b Д a.

3. Сочетательный (ассоциативный) закон:

— для логического сложения: ( A к B ) к C = A к ( B к C );

При одинаковых знаках скобки можно ставить произвольно или вообще опускать.

В обычной алгебре: (a + b) + c = a + (b + c) = a + b + c,

а Д ( b Д c ) = a Д ( b Д c ) = a Д b Д c .

4. Распределительный (дистрибутивный) закон:

— для логического сложения: ( A к B )& C = ( A & C ) к ( B & C );

— для логического умножения: ( A & B ) к C = ( A к C )&( B к C ).

Определяет правило выноса общего высказывания за скобку.

В обычной алгебре: (a + b) Д c = a Д c + b Д c.

5. Закон общей инверсии (законы де Моргана):

— для логического сложения = & ;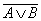

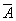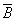— для логического умножения: 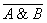= 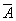к

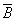
6. Закон идемпотентности ( от латинских слов idem — тот же самый и potens —сильный; дословно — равносильный):

— для логического сложения: A к A = A ;

— для логического умножения: A & A = A .

Закон означает отсутствие показателей степени.

7. Законы исключения констант:

— для логического сложения: A к 1 = 1, A к 0 = A ;

— для логического умножения: A &1 = A , A &0 = 0.

8. Закон противоречия: A& 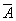= 0.

Невозможно, чтобы противоречащие высказывания были одновременно истинными.

9. Закон исключения третьего: A к 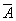= 1.

Из двух противоречащих высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

— для логического умножения: A &( A к B ) = A .

11. Закон исключения (склеивания):

— для логического сложения: ( A & B ) к ( 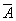& B ) = B ;

— для логического умножения: ( A к B )&( 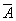к B ) = B .

12. Закон контрапозиции (правило перевертывания): ( A л B ) = ( B л A ).

Справедливость приведенных законов можно доказать табличным способом: выписать все наборы значений А и В, вычислить на них значения левой и правой частей доказываемого выражения и убедиться, что результирующие столбцы совпадут.

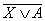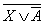Пример. Найдите X, если к = В.

Для преобразования левой части равенства последовательно воспользуемся законом де Моргана для логического сложения и законом двойного отрицания:

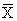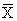( & ) к ( & A )

Согласно распределительному закону для логического сложения:

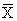&( к A )

Согласно закону исключения третьего и закона исключения констант:

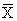&1 =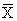

Полученную левую часть приравняем правой:

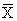= В

Окончательно получим, что X = .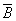

Пример 2. Упростите логическое выражение ( A к B к C )&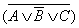

Правильность упрощения проверьте с помощью таблиц истинности для исходного и полученного логического выражения.

Согласно закону общей инверсии для логического сложения (первому закону Моргана) и закону двойного отрицания:

( A к B к C )& 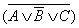= ( A к B к C )&( & B & )

Согласно распределительному (дистрибутивному) закону для логического сложения:

(A к B к C )&( &B& ) = (A& ) к (B& ) к (C& ) к (A&B) к (B&B) к (C&B) к (A& ) к (B& ) к (C& )

Согласно закона противоречия: ( A & ) = 0; ( C & ) = 0

Согласно закона идемпотентности ( B & B ) = B

Подставляем значения и, используя переместительный (коммутативный) закон и группируя слагаемые, получаем:

0 к ( A & B ) к ( & B ) к B к ( C & B ) к ( & B ) к ( C & ) к ( A & ) к 0

Согласно закона исключения (склеивания)

( A & B ) к ( & B ) = B

( C & B ) к ( & B ) = B

Подставляем значения и получаем:

0 к B к B к B к ( C & ) к ( A & ) к 0

Согласно закона исключения констант для логического сложения и закона идемпотентности:

Подставляем значения и получаем:

B к ( C & ) к ( A & )

Согласно распределительному (дистрибутивному) закону для логического умножения:

( C & ) к ( A & ) = ( C к A )&( C к )&( к A )&( к )

Согласно закона исключения третьего: ( C к ) = 1 ( к A ) = 1

Подставляем значения и окончательно получаем: B & & .

_02Л_Законы АЛ

Основные законы булевой алгебры

В алгебре логики аналогично обычной математике раскрытие сложных выражений подчиняется определённым законам. Сложные логические выражения выполняются в следующей последовательности:

Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.

Над логическими выражениями производят тождественные преобразования с использованием законов булевой алгебры.

Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.

Две эквивалентные функции, приравненные друг к другу, называются тождеством.

1. Переместительный закон (аналогично обычной алгебре):

От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.

2. Сочетательный закон (аналогично обычной алгебре):

Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции) при этом значение булевой переключательной функции не изменяется.

3. Распределительный закон

Распределительный закон здесь также справедлив, как и в обычной алгебре. Специфика его в булевой алгебре проявляется в некоторых частных случаях. Эти специфичные случаи и формулируются как распределительный закон булевой алгебры:

конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;

дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.

Справедливость распределительного закона для дизъюнкции докажем следующими простейшими преобразованиями:

В результате получаем

так как 1 v (b v c)=1 независимо от выражения в скобках.

4. Закон инверсии. Закон де Моргана.

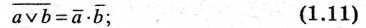
отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;

отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.

Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.

Таблица. Закон отрицания (де Моргана) для дизъюнкции

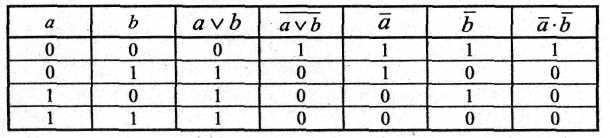
Таблица. Закон отрицания (де Моргана) для конъюнкции

Таблицы 1.5; 1.6 показывают, что на одинаковых наборах переменных значения функций совпадает. Законы де Моргана доказаны.

5. Законы повторения

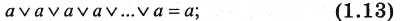
Многократное логическое сложение (логическое умножение) одной переменной равно самой этой переменной.

Законы повторения булевой алгебры существенно отличаются от законов повторения обычной алгебры.

6. Закон двойного отрицания

Двойное отрицание логической переменной равно самой логической перемененной.

7. Соотношения с нулем и единицей

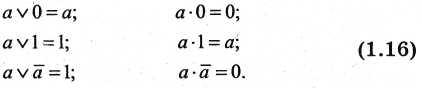
8. Закон склеивания:

Докажем законы склеивания эквивалентными преобразованиями

9. Законы поглощения

Доказательства законов поглощения

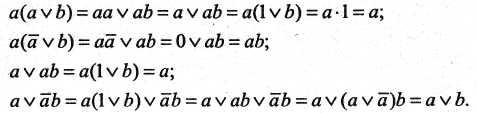
10. Умножение и сложение переменной и функции

Формулы умножения и сложения позволяют существенно упростить техническую реализацию логического устройства, заменить переменную некоторой константой: логической 1 либо логическим 0.

Правила алгебры логики позволяют преобразовать логическую функцию к виду, удобному для реализации в виде логического устройства.

Например, задана функция

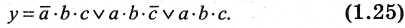
Для реализации функции в данном виде требуется два инвертора НЕ, три трехвходовых элемента ЗИ, один трехвходовый элемент ЗИЛИ (рис. 3).

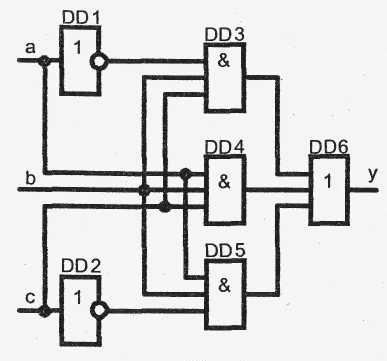
Проведем эквивалентные преобразования с использованием закона поглощения

Очевидно, что после преобразования функция значительно упростилась. Для реализации теперь достаточно иметь один двухвходовый элемент 2И, один двухвходовый элемент 2ИЛИ (рис.3). Обе схемы позволяют реализовать одну и ту же функцию.

Законы поглощения и склеивания. Основы формальной логики Законы поглощения и склеивания исключения

Стре́лка Пи́рса — бинарная логическая операция, булева функция над двумя переменными. Введена в рассмотрение Чарльзом Пирсом (Сharles Peirce) в 1880—1881 г.г.

Стрелка Пирса, обычно обозначаемая ↓, эквивалентна операции ИЛИ-НЕ и задаётся следующей таблицей истинности:

Таким образом, высказывание «X ↓ Y» означает «ни X, ни Y». От перемены мест операндов результат операции не изменяется.

11. Штрих Ше́ффера — бинарнаялогическая операция,булева функциянад двумя переменными. Введена в рассмотрениеГенри Шефферомв 1913 г. (вотдельных источниках именуется как Пунктир Чулкова) Штрих Шеффера, обычно обозначаемый |, эквивалентен операции И-НЕ и задаётся следующей таблицей истинности:

Таким образом, высказывание X | Y означает, что X и Y несовместны, т.е. не являются истинными одновременно. От перемены мест операндов результат операции не изменяется. Штрих Шеффера, как и стрелка Пирса, образует базис для пространства булевых функций от двух переменных. То есть используя только штрих Шеффера можно построить остальные операции. Например,

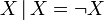—отрицание

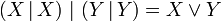— дизъюнкция

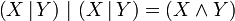— конъюнкция

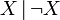— константа 1

В электронике это означает, что для реализации всего многообразия схем преобразования сигналов, представляющих логические значения, достаточно одного типового элемента. С другой стороны, такой подход увеличивает сложность реализующих логические выражения схем и тем самым снижает их надёжность. Примером может являться промышленная 155 серия.

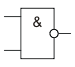
Элемент 2И-НЕ (2-in NAND), реализующий штрих Шеффера обозначается следующим образом (по стандартам ANSI):

В европейских стандартах принято другое обозначение:

12. Диодные ключи. Общие сведения. Электронный ключ — это устройство, которое может находиться в одном из двух устойчивых состояний: замкнутом или разомкнутом. Основу электронного ключа составляет нелинейный активный элемент (полупроводниковый диод, транзистор, тиристор и др.), работающий в ключевом режиме. По типу используемого нелинейного элемента электронные ключи делятся на диодные, транзисторные, тиристорные и т. д.

Диодные ключи. Простейший тип электронных ключей – диодные ключи. В качестве активных элементов в них используются полупроводниковые или электровакуумные диоды.

При положительном входном напряжении диод открыт и ток через него

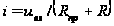, где 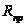– прямое сопротивление диода.

.

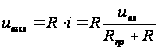Обычно 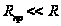, тогда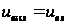. При отрицательном входном напряжении ток идет через диод

,

где – обратное сопротивление диода.

При этом выходное напряжение

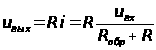. Как правило, 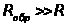и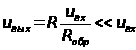. При изменении полярности включения диода график функции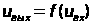повернется на угол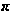вокруг начала координат.

Диодные ключи не позволяют электрически разделить управляющую и управляемые цепи, что часто требуется на практике. Для переключения (коммутации) напряжений и токов служат т.н. диодные ключи. Эти схемы позволяют при подаче определенного управляющего напряжения замыкать/размыкать электрическую цепь, по которой передается полезный сигнал (ток, напряжение). В простейших ключевых схемах в качестве управляющего может использоваться сам входной сигнал.

Говоря о диодных ключах нельзя не упомянуть особый класс полупроводниковых диодов — p-i-n-диоды. Они применяются только для коммутации ВЧ и СВЧ сигналов. Это возможно благодаря их уникальному свойству — регулируемой проводимости на частоте сигнала. Такое регулирование осуществляется обычно либо при подаче на диод внешнего постоянного напряжения смещения, либо непосредственно уровнем сигнала (для ограничительных p-i-n-диодов).

Источники:

http://lww-infproekt0405.narod.ru/Logika/Log.html
http://studfile.net/preview/2383572/
http://studfile.net/preview/3545493/page:3/